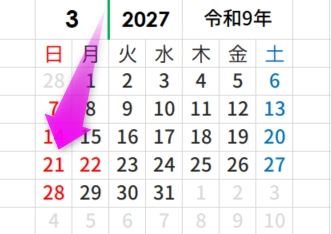
エクセルで春分の日･秋分の日を求める式

最終更新日 2025-12-26 19:56:05

エクセルで毎年､カレンダーを作成しているのですが､最もむずかしいのが祝日｡
いちいち内閣府のページで1つ1つ確認するのも大変｡
特に春分の日と秋分の日は､毎年決まった日ではなく､太陽と地球の位置関係によって決まるため､正確な日付は前の年の2月に発表されるらしいです｡
そこで今回は､エクセルで春分の日､秋分の日の近似値を求める式を紹介します｡2100年ぐらいまでならほぼ正確に春分の日･秋分の日を求めることが出来ます｡

春分の日を求める

そもそも春分の日とは？エクセルにおいて､単に式をコピペするだけでなく､きちんと祝日がどんな日で､どのような規則に沿っているのか理解していると､とても役立ちます｡

春分の日とは

春分の日とは､毎年3月20日または21日頃にある国民の祝日です。昼と夜の長さがほぼ等しくなる日で、天文学的には太陽が真東から昇り、真西に沈む日です。
この日を境に､夏至(昼が最も長い日)まで昼の時間が徐々に長くなっていきます｡

祝日法では「自然をたたえ、生物をいつくしむ」日とされています。

なぜ春分の日は毎年決まった日ではないのか？

春分の日が毎年変動(3月20日か21日､たまに19日)する理由は、地球の公転周期が365日ぴったりではないからです｡

地球が太陽の周りを1周するのに約365.2422日かかります｡つまり、365日と約6時間（正確には5時間48分46秒）
仮に､3月20日が春分の日だったとして､翌年には約6時間だけ3月21日に近づきます｡
4年間で約24時間のずれになります｡つまり､3月21日になる｡

これをリセットするのが｢うるう年｣｡4年に1度､2月に1日だけ追加(29日)して､この約24時間分を巻き戻します｡

ところが････

5時間48分46秒×4年 = 23時間15分4秒

44分56秒だけ短い････！？

3月19日が春分の日

そう､1年のずれは6時間きっかりではないので､4年に1度､24時間を加えると､実際には45分ほど巻き戻しすぎになります｡
きっかり昼の長さと夜の長さが同じ時間を｢春分点｣と呼ぶのですが､うるう年では､この春分点が45分ほど前倒し(3月19日に近づく)になります｡

で､2092年のうるう年では､とうとう巻き戻しが蓄積され､春分の日が若干前倒しになり､3月19日になります｡
(あとで実際に計算します)

うるう年のルール

うるう年のルール（グレゴリオ暦）

西暦が4で割り切れる年は「うるう年」。
ただし、100で割り切れる年は「平年（うるう年ではない）」。
ただし、400で割り切れる年は「うるう年」。

このルールの2番目により､蓄積された45分の前倒しもリセットされます｡
実際には2092～2100年の間に､3月19日が春分の日が何度か出るのですが､2100年は､

4で割り切れるが､100でも割り切れ､400では割り切れないので､平年(うるう年ではない)になり､うるう年の巻き戻しもリセットされます｡

1980年の春分の日を基準に計算

さて､1980年の春分点は､3月20日の20時14分04秒でした｡
そこでこの1980年3月20日20時14分04秒を基準にして､未来の春分の日を計算で求める｡これがエクセルで春分の日を求める式になります｡

春分の日を求める式

ここまで理解して式を眺めると､理解がしやすいと思います｡
さっそくエクセルで春分の日を求める式を紹介します｡

もとめる年を入力するセル

まず､春分の日を求めたい｢年｣を入力するセルを決めます｡
わかりやすいように｢A1｣のセルに入力します｡

で､春分の日の式を入力するセルを｢A3｣とします｡
こんな感じ｡

｢A3｣セルをクリックして､以下の式を入力します｡

= DATE(A1 , 3 , INT(20.8431 + 0.242194 * (A1 - 1980) - INT((A1 - 1980) / 4)))

DATA関数は､2027/03/20 というような年月日を返す関数です｡
第一引数に､A1のセルの｢年｣を代入し､第二引数は春分の日の｢月｣の｢3｣を代入しています｡

INT関数は､小数点以下を削除します｡

20.8431は､1980年3月20日20時14分04秒を日付にした値ですね｡
3月20.8431日

0.242194は､1年間は｢365日 + 0.242194日｣｡つまり､365日と0.242194日｡
1980年から求めたい｢年｣の差を計算し､この差に0.242194日をかけてやれば､どれくらい1980年の春分の日よりずれているかがわかります｡

ただし､うるう年で調整されるのでうるう年の回数を求め､引いてやります｡

例えば2027年の場合は････

 = DATA(2027 , 3 , INT(20.8431 - 0.242194 ×  47年 - 11年))
 = DATA(2027 , 3 , INT(20.8431 - 11.383118 - 11))
 = DATA(2027 , 3 , INT(20.8431 - 0.383118))
 = DATA(2027 , 3 , INT(20.459982))
 = DATA(2027 , 3 , 20)

つまり､2027年の春分の日は､3月20日ということがわかりました｡

西暦	春分の日
2020年	3月20日
2021年	3月20日
2022年	3月21日
2023年	3月21日
2024年	3月20日
2025年	3月20日
2026年	3月20日
2027年	3月21日
2028年	3月20日
2029年	3月20日
2030年	3月20日
2031年	3月21日

2024年はうるう年｡なので､再び3月20日に巻き戻されています｡
翌年からまた後ろにずれていき､2027年で3月21日にずれていますが､2028年がうるう年なので､再び3月20日に戻っています｡

次の3月19日は？

先ほど説明したように､うるう年で24時間巻き戻すのですが､24時間だと巻き戻しすぎ｡約45分ほど今度はうるう年ごとにはやくなっていきます｡
この45分が蓄積され､最初に3月19日に春分の日が来るのは､2092年になります｡

 = DATE( 2092 , 3 , INT(20.8431 + 0.242194 * ( 2092 - 1980 ) - INT(( 2092 - 1980 ) / 4) )
 = DATE( 2092 , 3 , INT(20.8431+ 0.242194 * 112 - 28))
 = DATE( 2092 , 3 , INT(20.8431 + 27.125728 - 28))
 = DATE( 2092 , 3 , INT(20.8431 -  0.874272))
 = DATE( 2092 , 3 , INT(19.968828))
 = DATE( 2092 , 3 , 19)

というわけで､2092年はギリギリ3月19日が春分の日になりました｡

西暦	春分の日
2092年	3月19日
2093年	3月20日
2094年	3月20日
2095年	3月20日
2096年	3月19日
2097年	3月20日
2098年	3月20日
2099年	3月20日
2100年	3月19日
2101年	3月20日
2102年	3月20日
2103年	3月20日
2104年	3月19日

うるう年対応版

今までの計算法では､2100年以降､何度も春分の日が3月19日になっています｡
先ほどの式は､｢うるう年のルール｣の｢100で割れる年はうるう年｣｢400で割り切れる年はうるう年」が組み込まれていません｡
2100年未満までの春分の日を求める場合は､先ほどの式でもOK｡

そこで以下が､うるう年ルール対応版になります｡

=DATE(A1 , 3 , INT(20.8431 + 0.242194 * (A1 - 1980) - (INT(A1 / 4) - INT(A1 / 100) + INT(A1 / 400) - 480)))

西暦	春分の日
2092年	3月19日
2093年	3月20日
2094年	3月20日
2095年	3月20日
2096年	3月19日
2097年	3月20日
2098年	3月20日
2099年	3月20日
2100年	3月20日
2101年	3月21日
2102年	3月21日
2103年	3月21日
2104年	3月21日

このように2100年以降は､しばらく3月21日が春分の日になる年が多くなります｡

さて､単純にその年の春分の日を求めるならこれで完成です｡が････
もし､エクセルでカレンダーを作成している場合､春分の日だけでなく､振替休日があるかも判定したい場合も考える必要があります｡

注意点

上で紹介したエクセルで春分の日を求める式は､あくまで1980年の春分の日を元に､ズレが一定であることを条件に計算で求める｢簡易式｣になります｡
ですが実際には様々な惑星の重力などによって､年月とともに別のズレも加わる可能性があるので､正確な春分の日は国立天文台のサイトで確認してください｡

振替休日対応版

祝日が日曜日に該当した場合､翌日の月曜日は振替休日というルールがあります｡
もし､春分の日が日曜日だった場合､その翌日の月曜日は振替休日と自動で判定して欲しい場合は以下｡

WEEKDAY関数は､第一引数に年月日を指定すると､曜日を1～7で返してくれる関数｡

曜日	戻り値
日曜日	1
月曜日	2
火曜日	3
水曜日	4
木曜日	5
金曜日	6
土曜日	7

つまり､先ほどの式で求められる春分の日をこの｢WEEKDAY関数｣に渡してやって､｢1｣が帰ってくればそれは日曜日だから､翌日の月曜日は振替休日｡

これを実現するには､

先ほどのセルを利用します｡
振替休日があるかないかB3で判定し､ある場合はその日付を表示します｡

=IF(WEEKDAY(A3) = 1 , A3 + 1 , "ありません")

IF関数は､第一引数で与えられた条件が成立(TRUE)した場合は､第二引数の値を｡
成立しない(FALSE)場合は､第三引数の値を代入します｡

つまり､春分の日が日曜日(=1)の場合は､春分の日に1を加えた日付を｡
｢1｣以外であれば｢ありません｣を代入します｡

例えば2027年だと､春分の日は､

このように日曜日になります｡なので振替休日がある｡

このような結果になります｡

2028年の場合は････

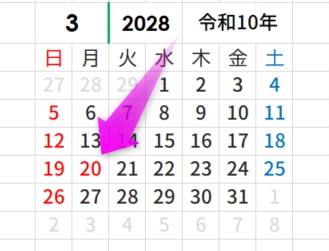ところがカレンダーを見てみると､月曜日が祝日になっている！！！？

そう､実は2028年は20日の月曜日が春分の日なのだ｡
振替休日ではなくて､単に春分の日が月曜日だっただけ｡

エクセルで秋分の日を求めるには

続いて秋分の日｡

秋分の日とは

秋分の日は､太陽が「秋分点」（天の赤道を北から南へ横切る瞬間）を通過する日です。
春分の日と同様、「昼と夜の長さがほぼ同じ」になります（実際には大気の屈折などで昼の方が14分ほど長いです）。
この日を境に夜が長くなっていき、「秋の夜長」へと向かいます。

「祖先をうやまい、亡くなった人々をしのぶ日」として、1948年に国民の祝日に定められました。

春分の日と同じで毎年決まった日が秋分の日ではなく､9月22日か23日のどれか｡時々9月24日も秋分の日になります｡(たぶん､生きているうちには9月24日が秋分の日になることはないでしょう)

秋分の日を求める式

エクセルで秋分の日を求める式は以下｡
うるう年のルールに対応したものになります｡

= DATE(A3 , 9 , INT(23.2488 + 0.242194 * (A3 - 1980) - (INT(A3 / 4) - INT(A3 / 100) + INT(A3 / 400) - 480)))

考え方は春分の日とまったく同じ｡1980年の秋分の日を基準に､ズレの合計を足し､うるう年のルールも取り入れて調節しています｡

春分の式では 20.8431 でしたが、秋分では 23.2488 を使います。これは1980年における秋分の日時（9月23日の約6時ごろ）を基準にしているためです。

なぜ春分と秋分で「.8431」や「.2488」のように定数が違うの？

地球の公転軌道は完全な円ではなく「楕円」をしています。
そのため、地球が太陽に近い時期と遠い時期で、公転するスピードが微妙に変わります。

春から夏：地球は太陽から遠い位置を走るため、速度が少し遅くなります。
秋から冬：地球は太陽に近い位置を走るため、速度が少し速くなります。

この速度差があるために、春分から秋分までの日数と、秋分から次の春分までの日数は同じにはなりません。その「季節ごとのスピードの差」が、数式内の定数の違いとして現れているのです。

9月24日が秋分の日になるのは？

上の式で求めると､最もはやい秋分の日が9月24日になるのは､2107年になりました｡
が､2つの説があって｡
2107年は､日本標準時（JST）に基づいた場合｡
ところが､世界時（ロンドンなど）の場合､ 2017年の秋分点は23日の15時（まだ23日）｡

日本標準時(JST)では､9時間のズレがあるので､日本時間（JST）： 23日の15時 + 9時間 = 24日の0時となります｡
また､先ほどの式は､簡易式の精度の限界でもあるので､年代が未来になるほど精度も不正確になる可能性があります｡

年間カレンダーへの応用

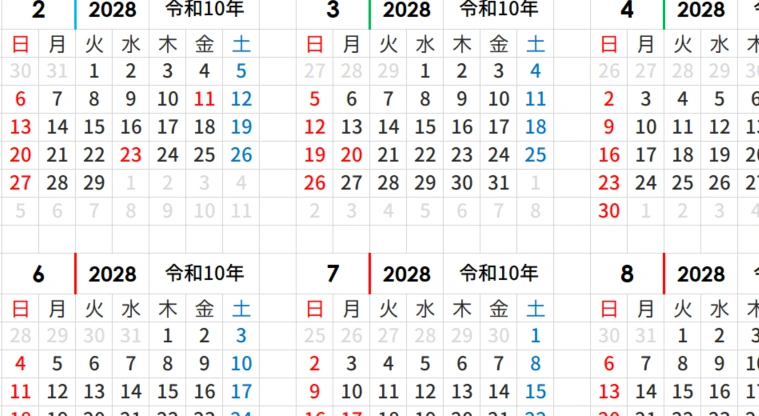年間カレンダーをエクセルで作成する場合､今回のような式はどのように活用すればよいのでしょうか？

エクセルでカレンダーを作成する場合は､まず､その年の祝日を埋める列を作成(画像のAJの列)し､その横に､振替休日がある場合は､祝日に＋1日の日付を埋めるようにします｡

カレンダーに｢祝日の場合は､数字を赤にする｣という条件にしたい場合は､この｢振替休日｣の列を参考にするようにします｡

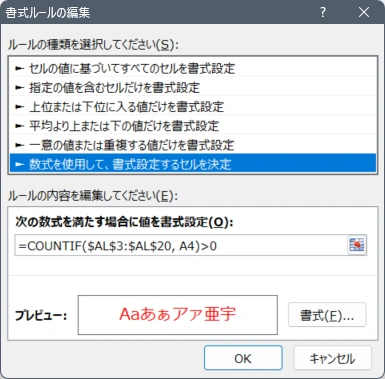カレンダー全体を選択状態にし､｢条件付き書式｣で､｢数式を使用して､書式設定するセルを決定｣で､

= COUNTIF($AL$3:$AL$20 , A4)>0

の条件に当てはまったら､フォントの色を赤にする｡

｢COUNTIF関数｣は､第一引数に与えられた範囲内に､第2引数の内容と同じものがいくつあるか数字を返す関数｡

もし､カレンダーの日付(365日)で｢振替休日｣のセルの中にマッチする｢日｣がある場合は､1を返します｡
振替休日のセルには､振替休日でなかった場合は祝日そのものを代入する式にします｡

=IF(WEEKDAY(AL3) = 1 , AL4 + 1 , AL4)

これは先ほど､春分の日が日曜日か確認する式｡
もし､WEEKDAY関数で｢1｣が帰ってきた場合は､その祝日は｢日曜日｣なので､日付に1を加える｡
｢1｣以外の数字が帰ってきた場合は､平日か土曜なのでそのまま祝日の日付を代入する｡

先ほどの書式のルールに戻って､｢>0(0より大きい)｣場合は､フォントが赤くなる｡

この祝日と振替休日の細かい使い方は､また別のページで取り上げます｡

エクセルで春分の日･秋分の日を求める式